АЛГЕБРА
Квадратні рівняння
Арифметична прогресія
Формули і властивості арифметичної прогресії.
Формули та властивості степенів
Число c називається n -тим степенем числа a якщо
| c = an = | a · a · ... · a |
| n |
Формули та властивості степенів використовуються під час операцій скорочення та спрощення складних виразів при розв'язанні рівнянь та нерівностей.
1. a0 = 1 (a ≠ 0)
2. a1 = a
3. an · am = an + m
4. (an)m = anm
5. anbn = (ab)n
6. a-n = 1an
7. anam = an - m
8. a1/n = n√a
Основні властивості коренів.
Формули скороченого множення.
Виведення формули квадрата суми
Для доказу справедливості формули квадрату суми достатньо перемножити вираз розкривши дужки:
Застосування формули квадрата суми
- для розкриття дужок
- для спрощення виразів
- для обчислення квадратів великих чисел, не використовуючи калькулятор або множення у стовпчик
Геометрична інтерпретація
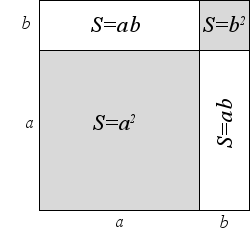
Формулу квадрату суми двох додатних чисел a та b можна зобразити геометрично
Розглянемо квадрат із стороною (a + b), його площа дорівнює (a + b)2.
У протилежних кутах квадрата, що розглядається, побудуємо квадрати зі сторонами a та b.
Тоді великий початковий квадрат буде розділений на чотири частини: два квадрати з площами a2 та b2 , а також два прямокутники з рівними площами ab. Тоді отримуємо, що
Приклади задач на застосування формули квадрата суми
Розв'язок:
Розв'язок:
Розв'язок:
Можна помітити, що вираз у чисельнику – це розкладений квадрат суми
Розв'язок:
Виведення формули квадрата суми
Для доказу справедливості формули квадрату суми достатньо перемножити вираз розкривши дужки:
Застосування формули квадрата суми
- для розкриття дужок
- для спрощення виразів
- для обчислення квадратів великих чисел, не використовуючи калькулятор або множення у стовпчик
Геометрична інтерпретація

Формулу квадрату суми двох додатних чисел a та b можна зобразити геометрично
Розглянемо квадрат із стороною (a + b), його площа дорівнює (a + b)2.
У протилежних кутах квадрата, що розглядається, побудуємо квадрати зі сторонами a та b.
Тоді великий початковий квадрат буде розділений на чотири частини: два квадрати з площами a2 та b2 , а також два прямокутники з рівними площами ab. Тоді отримуємо, що
Приклади задач на застосування формули квадрата суми
Розв'язок:
Розв'язок:
Розв'язок:
Можна помітити, що вираз у чисельнику – це розкладений квадрат суми
Розв'язок:
Різниця квадратів
Вивід формули різниці квадратів
Для доказу справедливості формули різниці квадратів достатньо перемножити вирази розкривши дужки:
Застосування формули різниці квадратів
- для розкриття дужок
- для спрощення виразів
Приклади завдань застосування формули квадрата різниці
Розв'язок:
Розв'язок:
Розв'язок:
Можна помітити, що для виразу у чисельнику можна використати формулу різниці квадратів
Виведення формули куба суми
Для доказу справедливості формули куба суми достатньо перемножити вираз розкривши дужки:
= (a + b)·(a2 + 2ab + b2) =
= a3 + 2a2b + ab2 + ba2 + 2b2a + b3 =
= a3 + 3a2b + 3ab2 + b3
Застосування формули куба суми
- для розкриття дужок
- для спрощення виразів
Приклади завдань застосування формули куба суми
Розв'язок:
= x3 + 9x2 + 27x + 27
Розв'язок:
= (2x)3 + 3·(2x)2·(3y2) + 3·(2x)·(3y2)2 + (3y2)3 =
= 8x3 + 36x2y2 + 54xy4 + 27y6
Розв'язок:
Можна помітити, що вираз у чисельнику – це розкладений куб суми, а у знаменнику – квадрат суми
Вивід формули куба різниці
Для доказу справедливості формули куба різниці достатньо перемножити вирази розкривши дужки:
= (a - b)·(a2 - 2ab + b2) =
= a3 - 2a2b + ab2 - ba2 + 2b2a - b3 =
= a3 - 3a2b + 3ab2 - b3
Застосування формули куба різниці
- для розкриття дужок
- для спрощення виразів
Приклади завдань застосування формули куба різниці
Розв'язок. Для вирішення скористаємося формулою куба різниці:
= x3 - 9x2 + 27x - 27
Розв'язок. Для вирішення скористаємося формулою куба різниці:
= (2x)3 - 3·(2x)2·(3y2) + 3·(2x)·(3y2)2 - (3y2)3 =
= 8x3 - 36x2y2 + 54xy4 - 27y6
Розв'язок:
Можна помітити, що вираз у чисельнику – це розкладений куб різниці, а у знаменнику – квадрат різниці
Виведення формули суми кубів
Для доказу справедливості формули суми кубів достатньо перемножити вираз розкривши дужки:
= a3 - a2b + ab2 + ba2 - ab2 + b3 = a3 + b3
Застосування формули суми кубів
- для розкладання на множники
- для спрощення виразів
Приклади завдань на застосування формули суми кубів
Розв'язок:
Розв'язок:
= (2x + 3y2)·(4x2 - 6xy2 + 9y4)
Розв'язок:
Можна помітити, що для виразу в чисельнику можна застосувати формулу суми кубів.
Вивід формули різниці кубів
Для доведення справедливості формули різниці кубів достатньо перемножити вирази розкривши дужки:
= a3 + a2b + ab2 - ba2 - ab2 - b3 = a3 - b3
Застосування формули різниці кубів
- для розкладання на множники
- для спрощення виразів
Приклади задач на застосування формули різниці кубів
Розв'язок:
Розв'язок:
= (2x - 3y2)·(4x2 + 6xy2 + 9y4)
Розв'язок:
Можна помітити, що для виразу у чисельнику можна застосувати формулу різниці кубів.
Основні формули
| 1. |
| ||
| 2. |
| ||
| 3. |
| ||
| 4. |
| ||
| 5. |
| ||
| 6. |
| ||
| 7. |
| ||
| 8. |
| ||
| 9. |
| ||
| 10. |
| ||
Загальні правила інтегрування функцій
| ∫ | c f(x) dx = c | ∫ | f(x) dx |
| ∫ | [ f(x) + g(x)] dx = | ∫ | f(x) dx + | ∫ | g(x) dx |
| ∫ | [ f(x) - g(x)] dx = | ∫ | f(x) dx - | ∫ | g(x) dx |
| ∫ | f(x)g(x) dx = f(x) | ∫ | g(x) dx - | ∫∫ | g(x) dx df(x) |
Інтеграли від раціональних функцій
Загальні формули диференціювання функцій
Таблиця похідних основних елементарних функцій
Похідна від константи
c ′ = 0, де c = constПохідна степеневої функції
(xn )′ = n · xn - 1Похідна показникової функції
(ax )′ = ax · ln aПохідна експоненти
(ex )′ = exПохідні логарифмів
Похідні тригонометричних функцій
| (tg x)′ = | 1 |
| cos 2 x |
| (ctg x)′ = - | 1 |
| sin 2 x |
Похідні обернених тригонометричних функцій
Формули площі трикутника
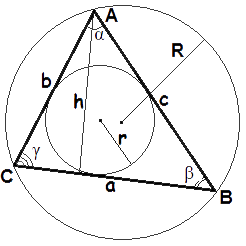
- Формула площі трикутника за стороною та висотою
Площа трикутника дорівнює половині добутку довжини сторони трикутника та довжини проведеної до цієї сторони висотиS = 1 a · h 2 - Формула площі трикутника за трьома сторонами
Формула Герона
S = √p(p - a)(p - b)(p - c) - Формула площі трикутника за двома сторонами і кутом між ними
Площа трикутника дорівнює половині добутку двох його сторін помноженого на синус кута між ними.
S = 1 a · b · sin γ 2 S = 1 a · c · sin β 2 S = 1 b · c · sin α 2 - Формула площі трикутника за трьома сторонам і радіусом описаного кола
S = a · b · с 4R - Формула площі трикутника за трьома сторонами і радіусом вписаного кола
Площа трикутника дорівнює добутку півпериметра трикутника на радіус вписаного кола.
S = p · r
де S - площа трикутника,
a, b, c - довжини сторін трикутника,
h - висота трикутника,
γ - кут між сторонами a и b,
r - радіус вписаного кола,
R - радіус описаного кола,
| p = | a + b + c | - півпериметр трикутника. |
| 2 |
Формули площі квадрата
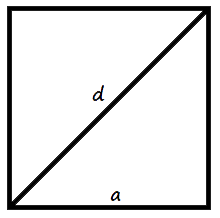
- Формула площі квадрата за довжиною сторони
Площа квадрата дорівнює квадрату довжини його сторони.
S = a2 - Формула площі квадрата за довжиною діагоналіде S - Площа квадрата,
Площа квадрата дорівнює половині квадрата довжини його діагоналі.
S = 1 d2 2
a - довжина сторін квадрата,
d - довжина діагоналей квадрата.
Формула площі прямокутника
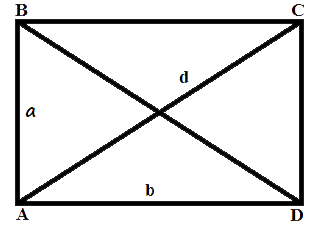
a, b - довжини сторін прямокутника.
Формули площі паралелограма
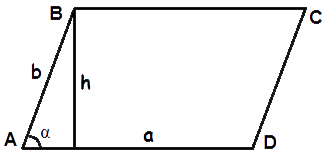
- Формула площі паралелограма за довжиною сторони і висоти
Площа паралелограма дорівнює добутку довжин його сторони і опущеної на цю сторону висоти.
S = a · h - Формула площі паралелограма за двома сторонами і кутом між ними
Площа паралелограма дорівнює добутку довжин його сторін помноженому на синус кута між ними.
S = a · b · sin α - Формула площі паралелограма за двома діагоналями і кутом між ними
Площа паралелограма дорівнює половині добутку довжин його діагоналей, помноженого на синус кута між ними.
S = 1 d1d2 sin γ 2
де S - площа паралелограма,S = 1 d1d2 sin γ 2
a, b - довжини сторін паралелограма,
h - довжина висоти паралелограма,
d1, d2 - довжини діагоналей паралелограма,
α - кут між сторонами паралелограма,
γ - кут між діагоналями паралелограма.
Формули площі ромба
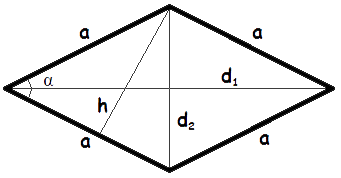
- Формула площі ромба за довжиною сторони і висоти
Площа ромба дорівнює добутку довжин його сторони і опущеної на цю сторону висоти.
S = a · h - Формула площі ромба за довжиною сторони і кутом
Площа ромба дорівнює добутку квадрату довжини його сторони і синуса кута між сторонами ромба.
S = a2 · sin α - Формула площі ромба за довжинами його діагоналейде S - площа ромба,
Площа ромба дорівнює половині добутку довжин його діагоналей.
S = 1 d1 · d2 2
a - довжина сторони ромба,
h - довжина висоти ромба,
α - кут між сторонами ромба,
d1, d2 - довжини діагоналей.
Формула площі трапеції
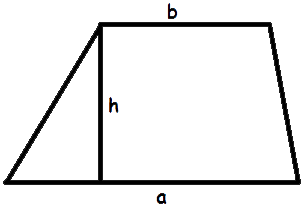
- Формула Герона для трапеції
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a - b| - Формула площі трапеції за довжиною основ і висотиде S - площа трапеції,
Площа трапеції дорівнює добутку півсуми її основ та висоти
S = 1 (a + b) · h 2
a, b - довжини основ трапеції,
c, d - довжини бокових сторін трапеції,
p = a + b + c + d - півпериметр трапеції. 2
Формули площі опуклого чотирикутника
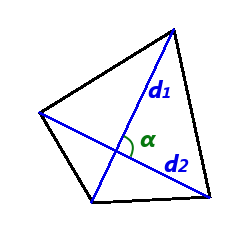
- Формула площі чотирикутника за довжинами діагоналей і кутом між нимиде S - площа чотирикутника,
Площа опуклого чотирикутника дорівнює половині добутку йог діагоналей помноженому на синус кута між ними:
S = 1 d1 d2 sin α 2
d1, d2 - довжини діагоналей чотирикутника,
α - кут між діагоналями чотирикутника. - Формула площі описаного чотирикутника (за довжиною периметру і радіусу вписаного кола)
Формули площі круга

- Формула площі круга через радіус
Площа круга дорівнює добутку квадрату радіуса та числа пі.
S = π r2 - Формула площі круга через діаметрде S - площа круга,
Площа круга дорівнює чверті добутку квадрата діаметра та числа пі.S = 1 π d2 4
r - довжина радіуса круга,
d - довжина діаметра круга.
Сфера, куля, сегмент.
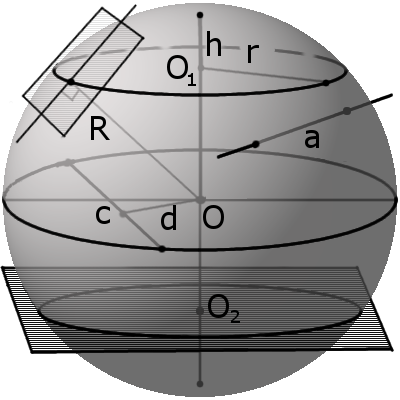
| V = | 4 | πR3 = | 1 | πD3 |
| 3 | 6 |
S = 4πR2 = πD2
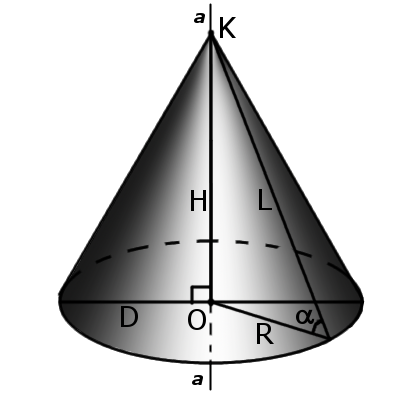
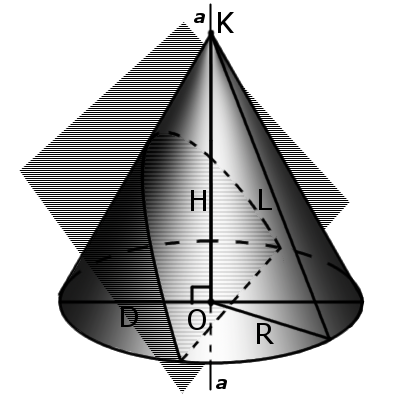
Конус.
Конус — це геометричне тіло, яке утворене сукупністю всіх променів, що виходять з точки та перетинають будь-яку плоску поверхню. В місці перетину утворюється основа конуса.
 |
 |
|
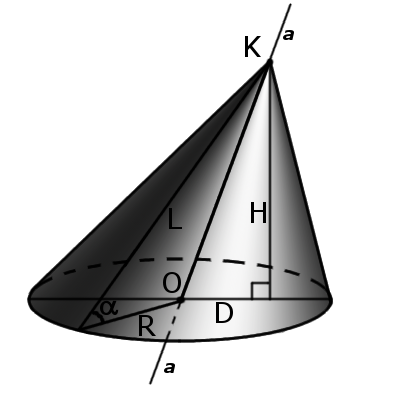
| Мал.1 | Мал.2 | |
 |
 |
|
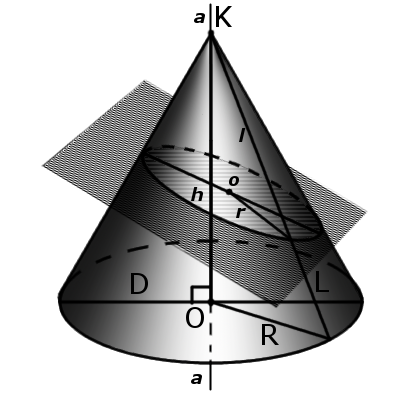
| Мал.3 | Мал.4 |
Елементи конуса
Бічна поверхня конуса - це сукупність усіх твірних конуса. Тобто, поверхня, яка утворюється рухом твірної по напрямній конуса.
Sb = πRL
Sp = πRL + πR2
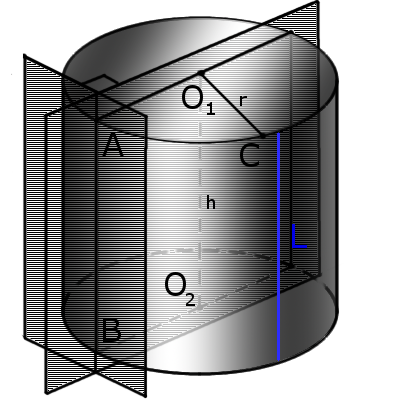
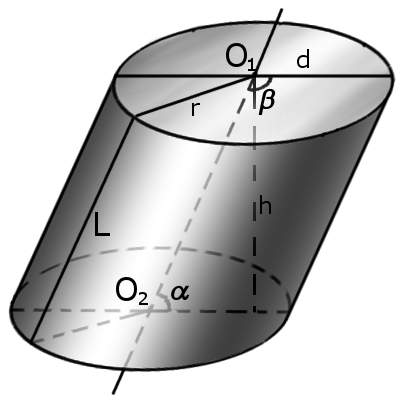
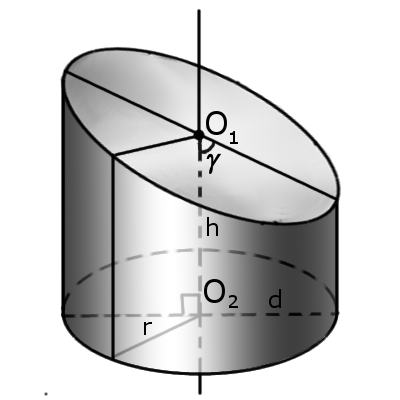
Циліндр
Циліндр — це геометричне тіло що обмежене циліндричною поверхнею та двома площинами основами циліндра.
 |
 |
 |
| V = πr2h = π | d2 | h , |
| 4 |
Sb = 2πrh = πdh
S = 2πr(h + r)
Немає коментарів:
Дописати коментар